Средние величины. Правовая статистика

метки: Среднее, Средний, Величина, Правовой, Статистик, Применение, Значение, Интервал

В качестве обобщающих показателей в статистике широко используются средние значения. Среднее значение является обобщающим показателем, характеризующим размер определенной переменной количественной характеристики в единицах качественно однородной совокупности в целом или для отдельных ее частей. Например, средний возраст лиц, осужденных за кражу. В правовой статистике средние величины используют для характеристики:

• — средних сроков рассмотрения дел данной категории;
• — среднего размера иска;
• — среднего числа ответчиков, приходящихся на одно дело;
• — среднего размера ущерба;
• — средней нагрузки судей и др.

Роль средних величин в статистике велика. В каждом явлении и в его развитии есть сочетание случайности и необходимости. При усреднении из-за действия закона больших чисел возможности уравновешиваются и уравновешивают друг друга. Именно благодаря применению средней величины статистика, имея дело с массовыми данными, получает возможность переходить от единичного к общему, от случайного — к закономер- ¹

Данные из Статистического сборника «Преступность и правонарушения» (2005— 2009).

М., 2010.

ному. Среднее значение является результатом абстрагирования от совокупности существующих различий в единицах измерения, но не заменяет конкретные индивидуальные значения. Но именно в этой абстракции, в способности абстрагироваться от случайности отдельных значений флуктуаций, и заключается научная ценность средних значений как обобщающих характеристик совокупностей.

Средние, исчисленные для явлений разного типа, подобны оценке «средней температуры по больнице» и носят фиктивный характер , затушевывая реальную тенденцию. Таким образом, статистическая методология противопоставляется усреднению «всех и вся», а статистическая наука разработала условия и требования для использования средних значений по отношению к социальным процессам, методы проверки показателей на их адекватность. Встречающаяся вульгарная трактовка средних величин по типу: «у директора зарплата миллион, а у остальных работников по 10 тысяч, значит, по этой лживой статистике, средняя зарплата на предприятии будет примерно 500 тысяч», — это не просто свидетельство абсолютной некомпетентности людей, говорящих подобные вещи, а корыстно-намеренное желание «подгонять» цифровые данные для достижения конъюнктурных целей. Действительно, любой средний показатель (при условии, что он рассчитан и проверен на адекватность в соответствии с правилами статистики) является не фиктивной конъюнктурной величиной, а важной обобщающей характеристикой общественных процессов¹ . Научный подход к исчислению средних величин предполагает, что для этого совокупность должна состоять из единиц, явлений, фактов одного и того же рода, т. е. быть качественно однородной, только тогда можно говорить об общем для всей совокупности «типе».

Статистика финансов

... сведения о финансовом состоянии организации Þ П4 - сведения о численности, заработной плате и движении работников. По данным формам средние и крупные ... Тема: “СНС как основа макроэкономической статистики” Переход к СНС государственной статистики вызван включением различных стран в ... доходы - 101,6 99 Средняя з/плата (тыс. руб) 938 119,5 164,7 Индекс инфляции (по потребительским ценам) 100,2* ...

Средняя всегда величина именованная и имеет ту же размерность , что и признак у отдельной единицы совокупности. Каждое среднее значение характеризует изучаемую совокупность по любому признаку переменной, поэтому за каждым средним значением стоит ряд распределений единиц этой совокупности согласно изучаемому признаку. В случаях, когда в генеральной совокупности имеются относительно однородные части и группы, необходимо рассчитать групповые средние. Общие и групповые средние значения отражают влияние различных условий: общее среднее отражает некоторые общие характеристики изучаемого явления, а средние по группе — уровень явления при более конкретных условиях.

Выбор типа среднего определяется содержанием показателя и исходными данными для расчета среднего. Все виды средних величин, используемые в статистических исследованиях, подразделяются на две категории: 1) степенные средние; 2) структурные средние. Первая категория средних величин включает: среднюю арифметическую , среднюю гармоническую, среднюю геометрическую и среднюю квадратическую. Вторая категория — это мода и медиана. При этом каждый из перечисленных видов степенных средних величин может иметь две формы: простую и взвешенную. Простая

форма средней величины используется для получения среднего значения изучаемого признака, когда расчет осуществляется по несгруппированяым статистическим данным либо когда каждый вариант в совокупности встречается только один раз. Взвешенными средними называют величины, которые учитывают, что варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на соответствующую частоту. Иными словами, каждый вариант «взвешивают» по своей частоте. Частоту называют статистическим весом.

Средняя арифметическая простая — самый распространенный вид средней. Вычисляется как частное от деления суммы значений всех вариантов на общее число единиц совокупности:

Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность (частоту).

В этом случае сложение всех значений количественного признака заменяется умножением варианта значения на ее соответствующую частоту (количество встречающихся вариантов):

где х_Ху х ₂ ,…, х_п — значения вариантов признака; /j,/₂ , — соответствующие им частоты или N — общее количество единиц.

Средневзвешенное арифметическое используется, когда данные представлены в виде серии вариаций или группировок. Она вычисляется как сумма произведений вариантов на соответствующие им частоты, деленная на сумму частот всех вариантов:

где Xj — значение i -го варианта признака; /, — частота /-го варианта.

Пример. Рассчитать среднее число судимостей, приходящихся на одного заключенного, используя следующие данные:

Число судимостей…1 2 3 4 5.

Число отбывающих наказание…85 71 42 12 1.

Решение. Для расчета используем формулу взвешенной средней арифметической:

Таким образом, в среднем на одного заключенного приходится 1,92 судимости.

Если вычисление средней величины производят, но данным, сгруппированным в виде интервальных рядов распределения, то сначала надо определить серединные значения каждого интервалах/, после чего рассчитать среднюю величину по формуле средней арифметической взвешенной, в которую вместо х, подставляют х/. В этом случае, если задана серия интервалов с первым и последним открытыми интервалами, значения этих интервалов принимаются равными значениям соседних закрытых интервалов.

Пример. по условным данным в таблице необходимо определить средний возраст лиц, незаконно пребывающих на территории РФ, выявленных в городе за отчетный период. 4.4.

Таблица 4.4

Распределение незаконно пребывающих на территории РФ лиц по возрасту.

Показатель.	Значение показателя.
Возрастная группа, лет.	До 18.	18−28.	29−39.	40 и более.
Число выявленных лиц.

Решение. Чтобы определить средний возраст этих особей на основе ряда вариаций интервалов, на первом этапе необходимо вычислить средние значения интервалов. Поскольку дана серия интервалов с первым и последним открытыми интервалами, значения этих интервалов будут приняты равными значениям соседних закрытых интервалов. Следовательно, в нашем случае значение первого интервала будет равно 8-18, а последнего — 40-50. Далее находим серединные значения интервалов: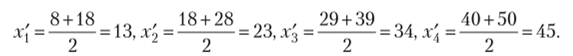

Теперь находим средний возраст выявленных лиц, но формуле средней арифметической взвешенной:

Таким образом, средний возраст лиц, обнаруженных в городе за отчетный период, незаконно пребывающих на территории Российской Федерации, составляет 28,9 года.

Простая средняя гармоническая представляет собой величин}’, обратную средней арифметической из обратных значений признака:

где 1 /X) — обратные значения вариантов; N — число единиц совокупности.

Пример. Для определения среднегодовой нагрузки на территориальные органы Минюста России по работе с обращениями граждан было проведено обследование пяти территориальных образований. Средние затраты времени на одну жалобу в указанных органах оказались равными (в днях): 3,1; 5,5; 2,3; 6,4; 4,6. Найдите среднюю стоимость одной жалобы гражданина для опрошенных местных органов Минюста России и среднегодовую нагрузку на орган при работе с жалобами граждан.

Решение. Для определения средних затрат времени на одну жалобу граждан применим формулу средней гармонической простой:

Тогда средняя годовая нагрузка при работе с жалобами граждан в расчете на один территориальный орган составит:

То есть территориальный орган рассматривает в среднем около 96 жалоб в год.

Если бы мы для определения средних затрат времени на одну жалобу граждан, воспользовались формулой средней арифметической простой, то получили бы.

Средняя годовая нагрузка на один территориальный орган составила бы: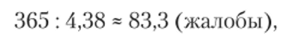

т.е. рассчитанная с помощью средней арифметической средняя нагрузка оказалась бы меньше той, что есть на самом деле. Для проверки правильности расчета, произведенного с помощью средней гармонической, воспользуемся исходными данными о затратах времени на одну жалобу для каждого территориального органа и рассчитаем число жалоб в абсолютном выражении, рассмотренных каждым из них за год: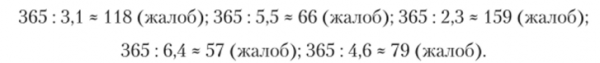

Теперь на основе полученных данных вычислим среднюю годовую нагрузку одного территориального органа при работе с жалобами граждан:

То есть полученная с использованием абсолютных значений средняя годовая нагрузка совпадает с величиной, полученной с использованием средней гармонической, что наглядно подтверждает необходимость использования в рассмотренном примере именно средней гармонической и недопустимость применения в данном случае средней арифметической.

В тех случаях, когда известны варианты признака, их объемные значения (произведение варианта на частоту), но неизвестны сами частоты, применяется формула взвешенной средней гармонической:

где x_i — значение i-го варианта признака; w_i — объемное значение г-го варианта (да, — = Xjfj).

Пример. Пусть имеются данные о трех группах преступлений, для каждой из которых характерна определенная сумма нанесенного потерпевшим ущерба (данные условные).

Требуется определить среднюю сумму ущерба от одного преступления (с учетом всех преступлений), используя следующие данные:

Номер группы преступлений…1 2 3.

Сумма ущерба, причиненного каждым преступлением группы, тыс. руб… 10 50 150.

Общая сумма ущерба, причиненного группой преступлений, тыс. руб…600 1000 1500.

Решение. Поскольку нам известна сумма ущерба от одного преступления по каждой группе (варианты признака) и общая сумма ущерба от всех преступлений по каждой группе (объемные значения), но неизвестны количества преступлений, входящих в каждую группу (частоты вариантов), то следует применить формулу средней гармонической взвешенной:

Если же для решения этой задачи мы попытались бы использовать формулу средней арифметической, то получили бы:

Как видим, неправильный выбор применяемого вида средней привел к результату, который отличается от истинного более чем в два раза (16, «https:// «).

Средняя геометрическая вычисляется извлечением корня степени N из произведения всех значений вариантов признака:

где x_lf х₂ , Хдг — индивидуальные значения варьирующего признака (варианты); N — число единиц совокупности.

Этот тип усреднения используется для расчета средних темпов роста временного ряда.

Рассмотрим использование среднего геометрического на традиционном примере расчета среднегодового темпа роста количества прав на недвижимое имущество, зарегистрированных на территории субъекта Российской Федерации в течение четырех лет. Условные исходные данные представляют собой значения показателя динамики количества зарегистрированных прав на недвижимость:

Год…1999 2000 2001 2002.

Годовой коэффициент роста…1,8 1,4 1,6 1,2.

Коэффициент роста в 2000 г., равный 1,4, означает, что в 2000 г. в данном субъекте РФ было зарегистрировано в 1,4 раза больше прав на недвижимость, чем в 1999 г. Требуется определить среднегодовой за четырехлетний период коэффициент роста количества зарегистрированных прав на недвижимость на территории данного субъекта РФ.

Попытка получить среднее значение коэффициента роста путем расчета простой средней арифметической из имеющихся четырех значений годовых темпов роста является методически ошибочной и приведет к неверному результату:

Корректно же выполненный расчет (т.е. с применением формулы средней геометрической) даст следующий результат:

Как видим, правильный результат (148,3%) действительно отличается от полученного некорректным методом неверного результата (150%).

Среднеквадратичный корень используется для вычисления дисперсии, которая является мерой вариации, которая будет рассмотрена ниже.

Для определения структуры совокупности используют особые средние показатели, к которым относятся медиана и мода или так называемые структурные средние. Если средняя арифметическая рассчитывается на основе использования всех вариантов значений признака, то медиана и мода характеризуют величину того варианта, который занимает определенное положение в ранжированном (упорядоченном) ряду. Упорядочивание единиц статистической совокупности может осуществляться в порядке возрастания или убывания вариантов изучаемого атрибута.

Медиана (Me) — величина, которая соответствует варианту, находящемуся в середине ранжированного ряда, или значение признака у средней единицы ранжированного ряда (значения признака, записанные в порядке возрастания или убывания).

Следовательно, медиана — это вариант ранжированного ряда, по обе стороны от которого должно быть равное количество единиц населения в данном ряду.

Чтобы найти медиану, вы должны сначала определить ее порядковый номер в ранжированном ряду по формуле.

где N — объем ряда (число единиц совокупности).

Если ряд состоит из нечетного числа членов, то медиана равна варианту с номером JV _Me . Если серия состоит из четного числа элементов, медиана определяется как среднее арифметическое двух соседних вариантов, расположенных посередине.

Пример. Пусть имеются следующие ранжированные сведения о количестве нотариусов, действующих в девяти населенных пунктах субъекта РФ: 7, 13, 21, 21, 29, 31, 45, 48, 87. Поскольку объем ряда N= 9, то N_Mc = (9 + 1)/2 = 5. Тогда, Me = 29, т. е. медиана равна пятому варианту, по обе стороны от которого расположены по четыре единицы ранжированного ряда. Если исходный ранжированный ряд содержал бы четное число значений (например, первые восемь из рассмотренного примера), то порядок расчета медианы был бы следующим: N= 8, следовательно, N_Me = (8 + 1)/2 = = 4,5, тогда медиана равна полусумме четвертого и пятого вариантов, т. е. Мс = (21 + + 29)/2 = 25.

В серии дискретных вариаций, содержащих, помимо значений опций, их частоты, медиана определяется накопленными частотами. Для этого сначала рассчитывается объем популяции, затем определяется медианное число, после чего частоты вариантов, начиная с первого, добавляются последовательно до тех пор, пока медианное число не будет превышено. Значение последнего просуммированного варианта и будет медианой.

Пример. Найдите медианное значение по «количеству обвинительных приговоров» на основе следующих данных, представленных в таблице. 4.5.

Таблица 45

Количество осужденных, имеющих судимости.

Показатель.	Значения показателей.
Число судимостей (варианты).
Число отбывающих наказание (частоты).

Решение. Объем статистической совокупности в данном примере составляет N = = (85 + 71 + 42 + 12 + 3) = 213, отсюда N_Me = (213+1)/2 = 107. Начав суммирование частот вариантов, представленных в этом примере, мы останавливаемся на втором варианте, поскольку сумма частот уже первых двух вариантов (85 + 71 = 156) превосходит рассчитанный нами номер медианы (107).

Следовательно, значение медианы Me = 2.

В серии изменения диапазона распределения сначала указывают диапазон, в котором будет найдена медиана. Его называют медианным. Это первый интервал, суммарная частота которого превышает половину объема интервального ряда вариаций. Затем численное значение медианы определяется по формуле.

где х _Мс — нижняя граница медианного интервала; i — величина медианного интервала (разность максимальной и минимальной границ интервала «от — до»); — накопленная частота интервала, который предшествует медианному (сумма значений в графах таблицы до графы, соответствующей медианному интервалу); /_Ме — частота медианного интервала (число в статистической таблице в медианном интервале).

Пример. Найти средний возраст выявленных в городе лиц за отчетный период, незаконно пребывающих на территории Российской Федерации, по условным данным в таблице. 4.4.

Решение. Поскольку доступные данные представляют собой серию интервалов распределения, на первом этапе необходимо определить средний интервал. Объем статистической совокупности N = 8 + 95 + 76 + 19 = 198, следовательно, медианным является интервал 18—28, так как это первый интервал, накопленная частота которого (8 + 95 = 103) превышает половину объема (198: 2 = 99).

Зная медианный интервал, подставляем в приведенную выше формулу соответствующие значения и получим:

Таким образом, половина выявленных лиц, незаконно пребывающих на территории РФ, младше 28 лет.

Модой (Мо) называют значение признака, которое наиболее часто встречается у единиц совокупности.

Мода используется для определения ценности наиболее распространенной характеристики. Для дискретной серии режимом будет вариант с наибольшей частотой. Например, для дискретного ряда, представленного в табл. 4.5, Mo = 1, так как этому значению варианта соответствует наибольшая частота — 85. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту).

Затем в этом диапазоне находится значение характеристики, которая может быть модой. Его значение находят по формуле.

где х_ш — нижняя граница модального интервала; i — величина модального интервала (разность максимальной и минимальной границ интервала «от — до»); /_Мо — частота модального интервала; /_Mo __t — частота интервала, предшествующего модальному; /_Мо+1 — частота интервала, следующего за модальным.

Пример. Определить моду возраста лиц, выявленных в городе, незаконно пребывающих на территории Российской Федерации, по данным, представленным в таблице. 4.4.

Решение. Модальным интервалом в нашем примере будет интервал «18—28 лет», так как ему соответствует наибольшая частота (95).

Для определения значения моды применим приведенную выше формулу, подставив в нее соответствующие данные из нашего примера:

Таким образом, возраст наибольшего числа выявленных лиц, незаконно пребывающих на территории РФ, составляет приблизительно 26 лет.

• Подробнее см.: Овчаров А. О. О роли статистической методологии в научных исследованиях // Вопросы статистики. 2014. № 4. С. 28.