Оптимизация — это деятельность, направленная на получение наилучших результатов при правильных условиях.
Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др).
Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев — невозможно.
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса, например:
количество продукции — расход сырья
количество продукции — качество продукции
Выбор варианта компромисса для указанных свойств — это процедура решения задачи оптимизации.
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации и цели оптимизации. При этом формулировка каждой задачи оптимизации должна требовать значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует другого.
2. Наличие ресурсов оптимизации, понимаемых как возможность выбора значений некоторых параметров оптимизируемого объекта.
3. Возможность количественной оценки оптимизированного значения, поскольку только в этом случае можно сравнивать эффекты выбора определенных управляющих воздействий.
4. Учет ограничений.
Обычно оптимизируемая величина связана с экономичностью работы рассматриваемого объекта (аппарат, цех, завод).
Оптимизированный вариант функционирования объекта следует оценивать количественным показателем — критерием оптимальности.
Критерий оптимальности — это количественная оценка оптимизируемого качества объекта.
На основе выбранного критерия оптимальности составляется целевая функция, которая представляет собой зависимость критерия оптимальности от параметров, влияющих на его значение. Тип критерия оптимальности или целевой функции определяется конкретной оптимизационной задачей.
Следовательно, задача оптимизации сводится к нахождению целевой функции.
Управление качеством продукции на предприятии
... результатах труда. 2. Принципы обеспечения качества и управления качеством продукции Управление качеством продукции - это установление, обеспечение и поддержание необходимого уровня качества продукции во время ее разработки, ... рыночной экономики. Конкурентоспособность можно определить как комплексную многоаспектную характеристику товара, определяющую его предпочтение на рынке по сравнению с ...
В зависимости от постановки любая задача оптимизации может быть решена различными методами и наоборот: любой метод может быть использован для решения многих задач. Методы оптимизации могут быть скалярными (оптимизация проводится по одному критерию), векторными (оптимизация проводится по многим критериям), поисковыми (включают методы регулярного и методы случайного поиска), аналитическими (методы дифференциального исчисления, методы вариационного исчисления и др.), вычислительными (основаны на математическом программировании, которое может быть линейным, нелинейным, дискретным, динамическим, стохастическим, эвристическим и т.д.), теоретико-вероятностными, теоретико-игровыми и др. Подвергаться оптимизации могут задачи как с ограничениями, так и без них.
Линейное программирование — одна из самых ранних и наиболее изученных областей математического программирования. Линейное программирование было разделом, из которого начала развиваться сама дисциплина «математическое программирование». Термин «программирование» в названии дисциплины ничего общего с термином «программирование (т.е. составление программ) для ЭВМ» не имеет, так как дисциплина «линейное программирование» возникла еще до того времени, когда ЭВМ стали широко применяться при решении математических, инженерных, экономических и др. задач. Термин «линейное программирование» произошел от неточного перевода английского «линейное программирование». Одно из значений слова «programming» — составление планов, планирование. Следовательно, правильным переводом «линейное программирование» было бы не «линейное программирование», а «линейное планирование», что более точно отражает содержание дисциплины. Однако, термин линейное программирование, нелинейное программирование и т.д. в нашей литературе стали общепринятыми.
Можно сказать, что линейное программирование применимо для математических моделей тех процессов, в основу которых может быть положена гипотеза линейного представления реального мира: экономических задач, задач управления и планирования, оптимального размещения оборудования и пр.
Задачи линейного программирования — это задачи, в которых целевая функция и ограничения в виде равенств и неравенств являются линейными. Вкратце, задачу линейного программирования можно сформулировать следующим образом: найти вектор значений переменных, которые обеспечивают линейную целевую функцию при m ограничениях в виде линейных равенств или неравенств.
Линейное программирование — наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи:
- рационального использования сырья и материалов;
- задачи оптимизации раскроя;
- оптимизации производственной программы предприятий;
- составления оптимального плана перевозок, работы транспорта;
- управления производственными запасами;
- и многие другие, принадлежащие сфере оптимального планирования.
Современные методы линейного программирования достаточно надежно решают общие задачи с несколькими тысячами ограничений и десятками тысяч переменных. Как правило, для решения очень больших задач используются специализированные методы.
В работе используются методы линейного программирования для решения производственной задачи
| Вид ресурса | число ресурсов, затрачиваемых на изготовление единицы продукции | всего ресурса | |
| P1 | P2 | ||
| S1 | 1 | 3 | 18 |
| S2 | 2 | 1 | 16 |
| S3 | 0 | 1 | 5 |
| S4 | 3 | 0 | 21 |
| прибыль от одной ед | 2 | 3 | |
Зная прибыль, полученную от продажи производственной единицы, и расход сырья для ее производства, необходимо разработать оптимальный производственный план, дающий максимальную прибыль. В этой статье мы решим эту проблему, используя классический симплексный метод, инструменты Excel и графические методы.
Глава 1. Решение задачи классическим симплекс методом
Коэффициенты целевой функции
![]()
Переменные целевой функции
![]()
Задача
![]()
при ограничениях
![]()
![]()
![]()
![]()
Введем фиктивные переменные Y, чтобы из неравенств сделать равенства
![]()
![]()
![]()
![]()
Введем в базис
![]()
Решим относительно базисных переменных

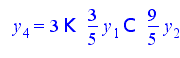
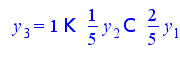
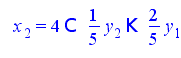
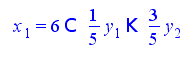
Запишем полученное решение в матричной форме
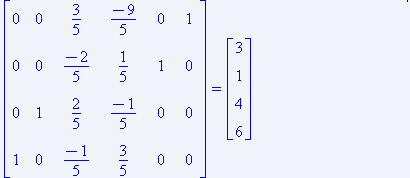
Коэффициенты относительных смещений для небазисных переменных отрицательны
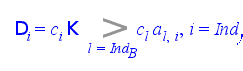
где ![]() -коэффициенты целевой функции при базисных переменных
-коэффициенты целевой функции при базисных переменных
![]()
а ![]() — множество индексов при свободных переменных
— множество индексов при свободных переменных
![]()
Поэтому указанный базис является оптимальным, а оптимальным решением является
![]()
Значение целевой функции
![]()
Глава 2. Графический метод
Максимизируем функцию
![]()
при ограничениях
![]()
![]()
![]()
![]()
![]()
![]()
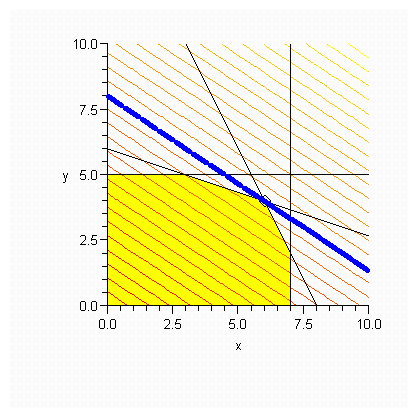
Максимум достигается в точке (отмечена ромбиком)
![]()
Значение целевой функции
![]()
Глава 3. Решение задачи с помощью Excel
Описание диалога «Поиск решений»
Решение можно использовать для решения проблем, связанных с множеством изменяемых ячеек, и помощи в поиске комбинаций переменных, которые максимизируют или минимизируют значение в целевой ячейке. Он также позволяет вам установить одно или несколько ограничений, условий, которые должны быть соблюдены при поиске решения. Поиск решения является
Поля ввода и кнопки в этом окне выполняют функции:
Установить целевую ячейку используется для указания целевой ячейки, значение которой должно быть увеличено, минимизировано или установлено равным указанному числу. Эта ячейка должна содержать формулу.
Равной служит для выбора варианта оптимизации значения целевой ячейки (максимизация, минимизация или подбор заданного числа).
Чтобы установить число, введите его в поле.
Редактируя ячейки, вы можете указать ячейки, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации для значения ячейки, указанного в поле «Установить целевую ячейку. Используется для автоматического поиска ячеек, которые влияют на формулу, указанную в поле «Установить целевую ячейку. Результат поиска отображается в поле Изменяя ячейки.
Ограничения используются для отображения списка граничных условий для действия.
Добавить отображает диалоговое окно Добавить ограничение.
Ссылка на ячейку используется для обозначения ячейки или диапазона, в котором вы хотите ограничить значения.
Ограничение используется для установки условия, которое применяется к значениям ячейки или диапазона, указанного в поле «Ссылка на ячейку. Выберите нужный условный оператор и введите число, формулу, ссылку на ячейку или ограничение диапазона в поле справа от раскрывающегося списка.
Добавить. Нажатие на эту кнопку позволяет принудительно задать новое условие для поиска решения проблемы, не возвращаясь в диалоговое окно «Поиск решения.
Правка отображает диалоговое окно «Редактировать ограничение. Содержимое этого окна точно такое же, как содержимое окна Добавить ограничение.
Удалить служит для снятия указанного ограничения.
Выполнить служит для запуска поиска решения поставленной задачи.
Close используется для выхода из диалогового окна без запуска поиска решения проблемы. В то же время настройки, сделанные в диалоговых окнах, которые появляются после нажатия кнопок «Параметры», «Добавить», «Изменить» или «Удалить», сохраняются.
Параметры отображает диалоговое окно Параметры решателя, в котором вы можете загрузить или сохранить модель для оптимизации и указать параметры для поиска решения.
Сброс используется для очистки полей диалогового окна и сброса параметров поискового решения к значениям по умолчанию.
Решение задачи
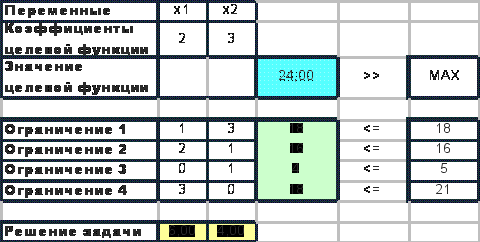
Средствами Excel мы получили, что надо произвести 6 ед. первой продукции и 4 ед. второй продукции. Максимальная выручка при этом равна 24.
Заключение
В задаче рассматриваются классические и программные методы решения задачи линейного программирования. Решение задачи во всех случаях было: произвести 6 ед. первой продукции и 4 ед. второй продукции. При этом прибыль составляла 24 ден.ед.
14
