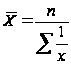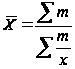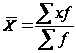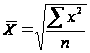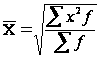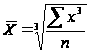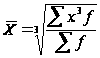История практического использования средних значений насчитывает десятки веков. Основной целью усреднения было изучение пропорций между значениями. Важность усреднения возросла в связи с развитием теории вероятностей и математической статистики. Решение многих теоретических и практических задач было бы невозможно без расчета среднего и оценки изменчивости отдельных значений признака.
Ученые разных направлений дать определение средней. Например, выдающийся французский математик О.Л.Коши (1789 — 1857) считал, что средней нескольких величин является новая величина, заключающаяся между наименьшей и наибольшей из рассматриваемых величин.
Однако создателем теории средних следует считать бельгийского статистика А. Кетле (1796 — 1874).
Он сделал попытку определить природу средних значений и закономерностей, которые в них проявляются. Согласно Кетле, постоянные причины действуют одинаково (постоянно) на каждое изучаемое явление. Именно они делают эти явления похожими друг на друга, создают для всех общие законы.
Следствием учения А. Кетле по общим и индивидуальным причинам было присвоение средних значений в качестве основного метода статистического анализа. Он указал, что средние статистические данные — это не просто мера математического измерения, но категория объективной реальности. Он отождествил типичное среднее, реально существующее, с реальной величиной, отклонения которой могут быть только случайными.
Ярким выражением изложенного взгляда на среднюю является его теория «среднего человека», т.е. человека среднего роста, веса, силы, среднего объема грудной клетки, емкости легких, средней и обычным цветом лица. Средние показатели характеризуют «истинный» тип человека, все отклонения от этого типа указывают на уродство или болезнь.
Взгляды А.Кетле получили дальнейшее развитие в работах немецкого статистика В.Лексиса (1837 — 1914).
Другой тип идеалистической теории средних значений основан на философии мачизма. Ее основатель английский статистик А. Боули (1869 — 1957).
В средних он видел простейший способ описать количественные характеристики явления. Определяя значение средних величин или, как он выражается, «их функцию», Боули выдвигает на первый план махистский принцип мышления. Итак, он написал, что функция средних значений ясна: она состоит в том, чтобы выразить сложную группу с помощью нескольких простых чисел. Ум не может сразу уловить величину миллионов статистических данных; они должны быть сгруппированы, упрощены, сведены к среднему значению.
Средние величины в статистике
... Кетле указывал, что смысл метода средних значений заключается в возможности перехода от единичного к общему, от случайного к регулярному, а наличие средних значений является категорией объективной реальности. «Понятие о средней величине ... повлечет за собой ограничение возможностей статистического анализа социальных процессов. Поэтому средние значения часто рассчитываются по разнородным явлениям. ...
Последователем А.Кетле был и итальянский статистик К.Джини (1884-1965), автор крупной монографии «Средние величины». К.Джини подверг критике определение средней, данное советским статистиком А.Я.Боярским, и сформулировал свое: «Средняя нескольких величин является результатом действий, выполняемых по определенному правилу над данными величинами, и представляет собой либо одну из данных величин, которая не больше и не меньше всех остальных (средняя действительная или эффективная), либо какую-либо новую величину, промежуточную между наименьшей и наибольшей из данных величин (счетная средняя)».
В данной курсовой работе мы подробно рассмотрим основные проблемы теории среднего значения. В первой главе мы раскроем суть средних значений и общие принципы применения. Во второй главе мы рассмотрим типы средних значений и их область применения на конкретных примерах. В третьей главе будут рассмотрены основные методологические требования к расчету средних значений.
1. Сущность средних величин, общие принципы применения
Средние значения являются одними из наиболее распространенных сводных статистических данных. Они стремятся охарактеризовать статистическую совокупность, состоящую из меньшинства единиц с номером. Средние величины тесно связаны с законом больших чисел.Суть этой зависимости заключается в том, что при большом количестве наблюдений случайные отклонения от общей статистики аннулируются и в среднем статистическая закономерность проявляется более отчетливо.
Среднее — это обобщенный показатель, характеризующий типичный уровень явления в определенных условиях места и времени. Он выражает уровень признака, характерный для каждой единицы населения.
Среднее значение является объективной характеристикой только для однородных явлений. Средства для гетерогенных популяций называются свипами и могут использоваться только в сочетании с частичными средствами для однородных популяций.
Среднее значение используется в статистических исследованиях для оценки преобладающего уровня явления, для сравнения нескольких популяций по одному и тому же критерию, для изучения динамики развития изучаемого явления во времени, для изучения взаимосвязей явлений.
Средние значения широко используются при планировании, прогнозировании и финансовых расчетах.
Главное значение средних величин состоит в их обобщающей функции, т.е. замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Всем известны особенности развития современных людей, проявляющиеся, в том числе, в большем росте сыновей, чем отцов, дочерей, чем матерей того же возраста. Но как измерить это явление?
В разных семьях очень разные пропорции роста старшего и младшего поколений. Далеко не всякий сын выше отца и не каждая дочь выше матери. Но если измерить средний рост многих тысяч лиц, то по среднему росту сыновей и отцов, дочерей и матерей можно точно установить как факт ускорения, так и типичное среднее увеличение роста на поколение.
На производство одного и того же количества товара определенного вида и качества разные производители (заводы, фирмы) затрачивают неодинаковое количество труда и материальных ресурсов. Но рынок усредняет эти затраты, а стоимость продукта определяется средним потреблением ресурсов для производства.
Стратегии роста для малых, средних и крупных фирм
... которых можно выделить три основных типа. наступления (атакующая) — стратегия завоевания и расширения рыночной доли. обороны — стратегия удержания существующей рыночной доли. отступления — стратегия сокращения рыночной доли с целью ... договором долю от суммы продаж в пользу крупной фирмы. Особенности стратегии роста средних фирм Средние компании находятся под давлением крупных и мелких компаний. Для ...
Время в одной точке мира в один и тот же день в разные годы может сильно отличаться. Например, в Санкт-Петербурге 31 марта температура воздуха за сто с лишним лет наблюдений колебалась от -20,1° в 1883 г. до +12,24° в 1920 г. Примерно такие же колебания и в другие дни года. На основе таких индивидуальных данных о погоде за несколько произвольных лет невозможно составить представление о климате Санкт-Петербурга. Характеристики климата — это средние за длительный период характеристики погоды — температуры воздуха, его влажность, скорость ветра, сумма осадков, число часов солнечного сияния за неделю, месяц и весь год и т.д.
Если среднее суммирует качественно однородные значения характеристики, то это типичная характеристика характеристики в данной совокупности. Так, можно говорить об измерении типичного роста русских девушек рождения 1973 г. по достижении ими 20-летнего возраста. Типичной характеристикой будет средняя молочная продуктивность коров черно-пестрой породы в первый год лактации при норме кормления 12,5 кормовых единиц в день.
Однако неправильно сводить роль средних значений только к характеристике типичных значений атрибутов в однородных популяциях для данного атрибута. На практике в современной статистике гораздо чаще используются средние значения, которые резюмируют явно разнородные явления, такие как, например, урожайность всех зерновых культур по России. Или рассмотрите средний показатель как среднее потребление мяса на душу населения: в конце концов, в эту группу входят дети до одного года, которые не потребляют мясо, вегетарианцы, северяне и южане, шахтеры, спортсмены и пенсионеры. Еще более очевидна нетипичность такого среднего показателя, как национальный доход в среднем на душу населения.
Средний национальный доход на душу населения, средний урожай зерна по стране, среднее потребление различных продуктов питания — это характеристики государства как единой национальной экономической системы, это так называемые системные средние.
Системные средние могут характеризовать как пространственные или объектные системы, существующие одномоментно (государство, отрасль, регион, планета Земля и т.п.), так и динамические системы, протяженные во времени (год, десятилетие, сезон и т.п.).
Примером системной средней, характеризующей период времени, может служить средняя температура воздуха в Санкт-Петербурге за 1992 г., равная +6,3°. Это среднее значение суммирует чрезвычайно неоднородные температуры морозных зимних дней и ночей, жарких летних дней, весны и осени. 1992 г. был теплым годом, его средняя температура не является типичной для Санкт-Петербурга. В качестве типической среднегодовой температуры воздуха в городе следует использовать многолетнюю среднюю, скажем, за 30 лет с 1963 по 1992 г., которая равна +5,05°. Эта средняя является типической средней, так как обобщает однородные величины; средние годовые температуры одного и того же географического пункта, варьирующие за 30 лет от +2,90° в 1976 г. до +7,44° в 1989 г.
Следовательно, типичное среднее может обобщать системные средние для однородной совокупности, или системное среднее может обобщать типичные средние для единственной, хотя и разнородной, системы.
Так, многолетняя средняя температура в Санкт-Петербурге в первые десятилетия и столетие существования города была значительно ниже; она возрастает медленно, но с ускорением за последнее столетие вследствие как роста самого города и энергопотребления в нем, что повышает температуру воздуха, так и начавшегося и ускоряющегося общего потепления на Земле. Следовательно, «типичность» любого среднего размера — понятие относительное, ограниченное как в пространстве, так и во времени.
Общие принципы применения средних величин:
- необходим обоснованный выбор единицы совокупности, для которой рассчитывается среднее значение;
- при расчете средней величины в каждом конкретном случае нужно исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков, а также имеющиеся для расчета данные;
- средние величины должны рассчитываться, прежде всего, по однородным совокупностям.
Качественно однородные совокупности позволяют получить метод группировок, который предполагает расчет не только среднего значения, но и системы обобщающих показателей;
— общие средние (средние для всей совокупности) должны подкрепляться групповыми средними. Например, анализ динамики урожайности отдельной сельскохозяйственной культуры показывает общее снижение урожайности по республике. Однако известно, что урожайность этой культуры зависит от почвенно-климатических, территориальных, экономических и других условий конкретного сельскохозяйственного года и различается в отдельных регионах. Сгруппировав регионы по уровню урожайности каждого года и проанализировав динамику групповых средних, можно обнаружить, что в отдельных группах регионов средняя урожайность либо не изменилась, либо даже возросла, но одновременно возросли удельный вес или число районов с более низкой урожайностью этой сельскохозяйственной культуры. Очевидно, что анализ факторов динамики средней группы позволяет более полно отразить тенденции изменения доходности по отношению к динамике общего среднего результата.
2. Виды средних величин и сфера их применения
Типы средних значений различаются, прежде всего, тем, в каком свойстве, какой параметр исходной переменной массы отдельных значений характеристики следует оставить неизменным.
В практике статистической обработки материала возникают разные проблемы, есть особенности изучаемых явлений, а значит, для их решения нужна разная информация.
Среднее значение, рассчитанное для населения в целом, называется общим средним, среднее значение, рассчитанное для каждой группы, называется средним значением группы. Общее среднее отражает общие характеристики изучаемого явления, среднее по группе дает характеристику масштабов явления, которое развивается в конкретных условиях данной группы.
Например, статистическое изучение рождаемости и среднего количества детей в семье на территории бывшего СССР проводилось в региональном аспекте (по союзным республикам).
Традиционно в Средней Азии и Закавказье рождаемость была выше, чем в центральных регионах России. Среднее количество детей в семье, рассчитанное для каждого региона, является среднегрупповым и, следовательно, рассчитанное по всей территории СССР, является общим средним.
На основе сравнительного анализа групповых и общих средств охарактеризованы социально-экономические типы изучаемого социального явления. В частности, при изучении рождаемости большое значение имеет характеристика этого процесса для социальных групп населения региона.
Групповые средние используются для изучения моделей развития социальных явлений. Так, в аналитических группировках анализ групповых средних позволяет сделать вывод о наличии и направлении взаимосвязи между группированным (факторным) признаком и результативном показателем.
Групповые средние значения также широко используются при определении имеющихся доступных производственных запасов, когда, помимо средних значений, также учитывается индивидуальная ценность признака.
Все средние величины делятся на два больших класса:
- степенные средние;
- к ним относятся такие известные и часто применяемые виды, как средняя арифметическая величина, средняя квадратическая и средняя геометрическая;
- средние величины, в качестве которых рассматриваются мода и медиана.
Средние значения мощности рассчитываются в двух формах: простой и взвешенный.
Простая средняя величина считается по несгруппированным данным и имеет вид:
,
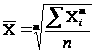где Xi – варианта (значение) осредняемого признака;
- m – показатель степени средней;
- n – число вариант (наблюдений).
Взвешенная средняя величина считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения:
,
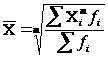где Xi – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
- m – показатель степени средней;
- fi – частота, показывающая, сколько раз i-e значение осредняемого признака.
Возьмем для примера расчет среднего возраста студентов в группе из 20 человек.
Таблица 2.1
|
№ п/п |
Возраст (лет) |
№ п/п |
Возраст (лет) |
№ п/п |
Возраст (лет) |
№ п/п |
Возраст (лет) |
|
1 |
18 | 6 | 20 | 11 | 22 | 16 | 21 |
|
2 |
18 | 7 | 19 | 12 | 19 | 17 | 19 |
|
3 |
19 | 8 | 19 | 13 | 19 | 18 | 19 |
|
4 |
20 | 9 | 19 | 14 | 20 | 19 | 19 |
| 5 | 19 | 10 | 20 | 15 | 20 | 20 | 19 |
Средний возраст рассчитаем по формуле простой средней:
Сгруппируем исходные данные. Получим следующий ряд распределения:
Таблица 2.2
| Возраст, X лет | 18 | 19 | 20 | 21 | 22 | Всего |
| Число студентов | 2 | 11 | 5 | 1 | 1 | 20 |
В результате группировки получаем новый показатель — частоту, указывающую число студентов в возрасте X лет. Следовательно, средний возраст студентов группы будет рассчитываться по формуле взвешенной средней:
Общие формулы расчета степенных средних имеют показатель степени (m).
В зависимости от того, какое значение он принимает, различают степенных средних:
- средняя гармоническая, если m = — 1;
- средняя геометрическая, если m → 0;
- средняя арифметическая, если m = 1;
- средняя квадратическая, если m = 2;
- средняя кубическая, если m = 3.
Если рассчитать все типы средних для одних и тех же исходных данных, их значения будут неодинаковыми. Здесь действует правило мажорантности: с увеличением показателя степени т увеличивается и соответствующая средняя величина:
Xгарм ≤ Xгеом ≤ Xарифм ≤ Xквадр ≤ Xкуб.
Пользуясь этим правилом, статистика может в зависимости от настроения и желания ее «знатока» либо «утопить», либо «выручить» студента, получившего на сессии оценки 2 и 5. Каков его средний балл?
Если судить по средней арифметической, то средний балл равен 3,5. Но если декан желает «утопить» несчастного и вычислит среднюю гармоническую
,
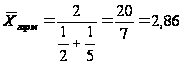то студент остается и в среднем двоечником, не дотянувшим до тройки. Однако студенческий комитет может возразить декану и представить среднюю кубическую величину:
.
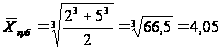Студент уже выглядит «хорошистом» и даже претендует на стипендию! И только в том случае, если лентяй провалил оба экзамена, статистика помочь не в состоянии: увы, все средние из двух двоек равны все той же двойке!
Формулы степенных средних величин приведены в табл. 2.3
В формулах средних значений п — это число единиц совокупности (число индивидуальных значений осредняемого признака X); х — индивидуальное значение признака у каждой единицы. Если совокупность объектов распределена по группам разной численности, то х — это значение признака, общее для всей группы; f — численность группы (частота повторения данного значения признака).
Формулы средних величин
| Вид степенной средней | Показатель степени(m) | Формулы расчета средней | |
| простой | взвешенной | ||
| Гармоническая | -1 |
|
m=xf |
| Геометрическая | → 0 |
|
|
| Арифметическая | 1 |
|
|
| Квадратическая | 2 |
|
|
| Кубическая | 3 |
|
|
2.1 Степенные средние величины
2.1.1 Средняя арифметическая величина
Среднее арифметическое — это такое среднее значение характеристики, при вычислении которого общая сумма характеристики в совокупности остается неизменной.
В противном случае мы можем сказать, что среднее арифметическое — это средний член. При его вычислении общий объем атрибута мысленно распределяется поровну между всеми единицами населения.
Среднее арифметическое является наиболее распространенным на практике типом усреднения. Различают 2 вида арифметических средних:
- Невзвешенную (простую);
- Взвешенную.
Средняя арифметическая невзвешенная рассчитывается для несгруппированных данных по формуле:
.
Для массовых статистических совокупностей рассчитывается взвешенная средняя арифметическая по формуле:
.
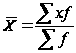Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, т.е. исходят из гипотезы о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые имеются, значения атрибутов должны определяться экспертным заключением на основе сущности, свойств атрибута и совокупности. Например, по табл.2.1.1 можно минимальный возраст рабочих считать 17 лет. Тогда первый интервал будет от 17 до 20 лет, а максимальный возраст — 65 лет, тогда последний интервал — 50-65 лет.
Распределение рабочих предприятия по возрасту
| Группы рабочих по возрасту, лет | Число рабочих fj | Середина интервала xj | xj fj |
| До 20 | 48 | 18,5 | 888 |
| 20-30 | 120 | 25 | 3000 |
| 30-40 | 75 | 35 | 2625 |
| 40-50 | 62 | 45 | 2790 |
| Старше50 | 54 | 57,5 | 3105 |
| Итого | 359 | 34,56 | 12408 |
Средний возраст рабочих, рассчитанный по формуле с заменой точных значений признака в группах серединами интервалов, составил:
= 
,
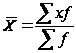что и записано в итоговую 3 табл.2.1.1.
Средняя арифметическая величина обладает рядом свойств, позволяющих ускорить расчет:
Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т. е. 
.
Это свойство определено требованиями правильного исчисления средней, согласно которым конкретные значения варьирующего признака уравниваются без изменения общего объема его и заменяются одним средним числом, которое как постоянный множитель выносится из-под знака суммы. Благодаря этому свойству среднее значение может использоваться для различных типов плановых и статистических расчетов как репрезентативное или заменяющее для всех значений атрибута переменной. Так, если средний расход горючего на 1 гектар пахоты составляет 20 литров, а всего надо вспахать 2 млн. га, то всего потребуется 40 млн. литров горючего. Аналогично, если достаточно репрезентативное выборочное обследование показало, что среднегодовой надой молока на одну корову составляет 2500 литров, а всего в районе 15 тыс. коров, то общий надой составит 37,5 млн. литров.
Сумма отклонений вариантов как от простой, так и от взвешенной средней арифметической равна нулю:
и 
Рассматриваемое свойство может быть использовано для проверки правильности вычисления среднего значения. Если при исчислении средней арифметической 
и 
не равны нулю, это указывает, что средняя неправильно исчислена. А поскольку при анализе часто необходимо использовать отклонения от среднего, их удобно использовать для проверки правильности вычисления среднего.
Сумма квадратов отклонений вариантов как от простой, так и от взвешенной средней меньше суммы квадратов отклонений от любой другой произвольной величины а, т. е.
.
Пример:
Таблица 2.1.2
| Табельный номер рабочего | 1 | 2 | 3 | 4 | 5 | 6 |
| Часовая выработка деталей (x) | 12 | 10 | 6 | 10 | 12 | 10 |
В примере, основанном на данных табл. 2.1.2, 
, а
При а =12 
составит:
Таблица 2.1.3
|
xi |
— a |
|
|
|
12 |
-12 | 0 |
0 |
|
10 |
-12 | -2 |
4 |
|
6 |
-12 | -6 |
36 |
|
10 |
-12 | -2 |
4 |
|
12 |
-12 | 0 |
0 |
|
10 |
-12 | -2 |
4 |
|
Итого |
48 |
Как видим, 24<48.
Если все частоты разделить (или умножить) на произвольное число (а), то средняя от этого не изменится, так как
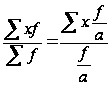
Если разгруппировать рабочих (табл.2.1.2) по числу выработанных за час деталей, получим такие данные (табл.2.1.4):
Таблица 2.1.4
| Варианты выработки деталей за час (x) | Число рабочих с данной выработки (f) | Объем варьирующего признака (xf) |
| 6 | 1 | 6 |
| 10 | 3 | 30 |
| 12 | 2 | 24 |
| Итого | 6 | 60 |
Если применить полученную формулу, к примеру, приведенному в табл. 2.1.4, это означает, что если, например, частоты уменьшить в 6 раз, средняя взвешенная арифметическая не изменится и будет равна:
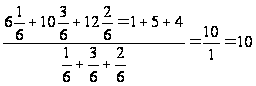
Средняя не изменится, если мы частности выразим в процентах, т. е. умножим их на 100:
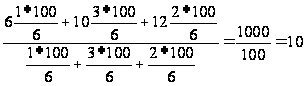
Рассматриваемое свойство показывает, что для этих вариантов характеристики значение среднего зависит не от абсолютного размера весов, а от соотношения между ними. В приведенном примере мы сначала уменьшили частоты в 6 раз, затем увеличили в 100 раз, но средний выход не изменился.
Если веса всех вариантов равны между собой, то взвешенная средняя равна простой средней, так как при этих условиях
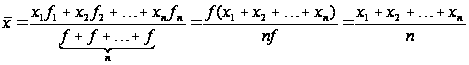
Поскольку вычисление простого арифметического среднего требует меньше работы, чем средневзвешенного, при равных весах нет необходимости использовать последнее.
Средняя алгебраической суммы равна алгебраической сумме средних. Так, если у, х и z — положительные варьирующие величины и уi =xi +zi , то
.
Следовательно, 
.
Это свойство среднего показывает, в каких случаях средства могут быть добавлены напрямую. Например, если продукт состоит из двух частей, изготовленных разными рабочими, и в то же время одна из них занимает в среднем 20 минут на одну деталь и 30 минут на другую, тогда в среднем 20 + 30 = 50 минут тратятся на продукт. Аналогичным образом решился бы вопрос, если бы продукт состоял из трех и более частей.
2.1.2 Средняя гармоническая величина
Если в соответствии с условиями задачи необходимо, чтобы сумма значений, обратных отдельным значениям атрибута, оставалась неизменной в течение среднего, то среднее значение является гармоническим средним.
Гармоническое среднее, как и среднее арифметическое, может быть простым и взвешенным. Если веса у каждого значения признака равны, то можно использовать среднюю гармоническую простую:
.
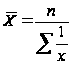Однако в статистической практике чаще применяется средняя гармоническая взвешенная:
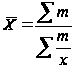, где m = xf ,
она используется, как правило, при расчете общей средней из средних групповых.
Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. m = Xf).
К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия.
Приведем расчет средней гармонической величины — простой и взвешенной.
Пример. Четыре швеи-надомницы заняты пошивом головных уборов одной модели. Первая швея тратит на изготовление одного головного убора 30 мин, вторая — 40 мин, третья — 50 мин, четвертая — 60 мин. Определим средние затраты времени на пошив одного головного убора при условии, что каждая швея работает по 10 ч в день.
Попытка решить задачу с помощью средней арифметической простой
оказалась бы успешной, если бы каждая надомница шила только по одному головному убору в день. В данном
