Графическое представление данных в статистике

метки: График, Таблица, Статистический, Статистик, Скачать, Явление, Данные, Построение

	Скачать реферат: Графическое представление данных в статистике

1. Понятие о статистическом графике. элементы статистического графика

Современную науку невозможно представить без применения графиков. Они стали средством научного обобщения.

Выразительность, четкость, лаконичность, универсальность, наглядность графических изображений сделали их незаменимыми в исследовательской работе и в международных сопоставлениях социально-экономических явлений.

Впервые о технике составления статистических графиков упоминается в работе английского экономиста У. Плейфейра «Коммерческий и политический атлас», опубликованной в 1786 г. и положившей начало развитию приемов графического изображения статистических данных.

семиотики,

Знак в семиотике служит символическим выражением определенных явлений, свойств или отношений.

Существующие знаковые системы в семиотике принято делить на неязыковые и лингвистические.

Неязыковые знаковые системы, Языковые знаковые системы

В лингвистических знаковых системах различают естественные и искусственные знаковые системы или языки.

естественный язык.

Искусственные языковые системы

Не исключая естественного языка, искусственные или символические языки упрощают представление специальных проблем в определенной области знаний.

статистический график

Значение графического метода в анализе и обобщении данных велико. Графическое изображение прежде всего позволяет осуществить контроль достоверности статистических показателей, так как, представленные на графике, они более ярко показывают имеющиеся неточности, связанные либо с наличием ошибок наблюдения, либо с сущностью изучаемого явления. С помощью графического изображения можно изучить закономерности развития явления, установить существующие связи. Простое сопоставление данных не всегда дает возможность уловить наличие причинных зависимостей, в то же время их графическое изображение способствует выявлению причинных связей, в особенности в случае установления первоначальных гипотез, подлежащих затем дальнейшей разработке. Графики также широко используются для изучения структуры явлений, их изменений во времени и их положения в пространстве. В них более выразительно проявляются сравнительные характеристики и отчетливо видны основные тенденции развития и взаимосвязи, присущие изучаемому явлению или процессу.

При построении графического изображения необходимо соблюдать ряд требований. Прежде всего, график должен быть достаточно наглядным, поскольку весь смысл графического изображения как метода анализа заключается в визуальном представлении статистических показателей. Кроме того, график должен быть выразительным, доходчивым и понятным. Для выполнения вышеперечисленных требований каждый график должен включать ряд ос-ковных элементов: графический образ; поле графика;

• пространственные ориентиры;
• масштабные ориентиры;
• экспликацию графика.

Графический образ (основа графика), Поле графика, Пространственные ориентиры

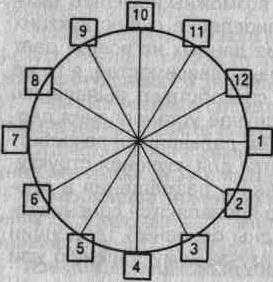
рис 5.1

радиусом.

Масштабные ориентиры, Масштабной шкалой

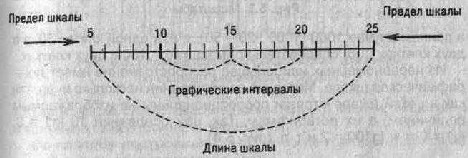
Рис. 5.2. Числовые интервалы

шкалы прямолинейные

равномерной.

длина отрезка

Как правило, масштаб определяется приблизительной оценкой возможной длины шкалы и ее границ. Например, на поле в 20 клеток надо построить шкалу от 0 до 850. Так как 850 не делится удобрю на 20, то округляем число 850 до ближайшего удобного числа, в данном случае 1000 (1000 : 20 = 50), т. е. в одной клетке 50, а в двух клетках 100; следовательно, масштаб — 100 в двух клетках.

Рис. 5.3.

Среди неправильных наиболее распространена логарифмическая шкала. Техника его построения немного отличается, так как на этой шкале сегменты пропорциональны не отображаемым значениям, а их логарифмам. Так, при основании 10 1д1 = О-1д1 = 0 = 1; 1д100 = 2 и т. д. (рис. 5.4).

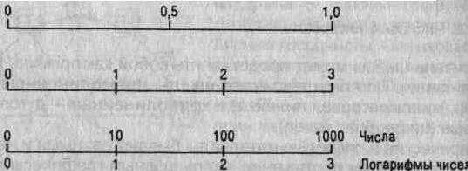
экспликация.

2. Классификация видов графиков

Существует множество видов графических изображений (рис. 5.5; 5.6).

Их классификация основана на ряде признаков: а) способ построения графического образа; б) геометрические знаки, изображающие статистические показатели; в) задачи, решаемые с помощью графического изображения.

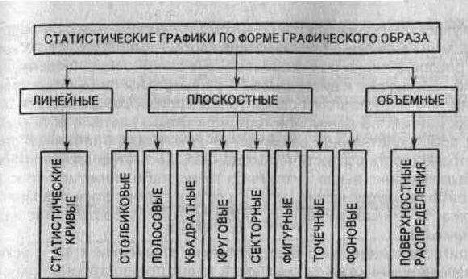
Рис. 5.5.

По способу построения, Геометрические знаки

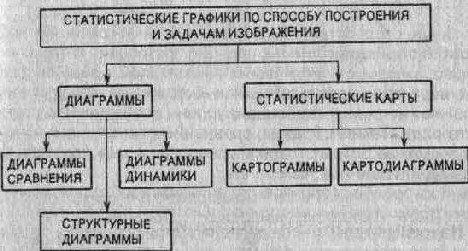
Рис. 5.6.

При построении точечных диаграмм в качестве графических образов применяются совокупности точек; при построении линейных — линии. Основной принцип построения всех плоских диаграмм заключается в том, что статистические величины представлены в виде геометрических фигур и, в свою очередь, разделены на полосы, полосы, круги, квадраты и завитки.

Статистические карты графически разделены на картограммы и картодиаграммы.

В зависимости от круга решаемых задач

Особым типом графиков являются диаграммы распределения величин, представленные сериями вариаций. Это гистограмма полигон, огива, кумулята.

3. Диаграммы сравнения

столбиковые диаграммы,

При создании гистограмм необходимо нарисовать прямоугольную систему координат, в которой расположены столбцы. Основания колонн располагаются на горизонтальной оси, размер основания определяется произвольно, но устанавливается одинаково для всех.

Шкала, определяющая масштаб столбиков по высоте, расположена по вертикальной оси. Вертикальный размер каждой полосы соответствует размеру статистики, отображаемой на графике. Следовательно, для всех столбцов, составляющих диаграмму, только одно измерение является переменным. Покажем построение столбиковой диаграммы по данным табл. 5.1, характеризующим вклады граждан в учреждения Сбербанка в 1995 г. (рис. 5.7).

Таблица 5.1

Вклады граждан в учреждения Сбербанка в 1995 г. (цифры условные)

Месяц	1	2	3	4	5	6	7	8	9	10	11	12
Вклад,	550	560	560	640	640	1100	1100	1100	1630	1610	1610	2500
млрд. руб.

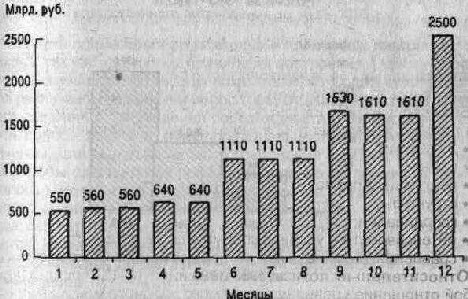
В соответствии с изложенными выше правилами на горизонтальной оси размещаются основания двенадцати столбиков на Одинаковом расстоянии друг от друга, в данном случае 0,5 см. ширина столбиков принята 0,5 см. Масштаб на оси ординат — 500 млрд. руб. — 1 см. Четкость этой диаграммы достигается путем сравнения размеров стержней.

• на одинаковом расстоянии друг от друга (рис. 5.7);
• вплотную друг к другу (рис. 5.8);
• в частном наложении друг на друга (рис.

5.9).

Рис. 5.8.

Рис. 5.9.

Правила построения гистограмм допускают одновременное расположение нескольких индикаторов на одной горизонтальной оси изображений. В этом случае столбики располагаются группами, для каждой из которых может быть принята разная размерность варьирующих признаков (рис. 5.10).

ленточные

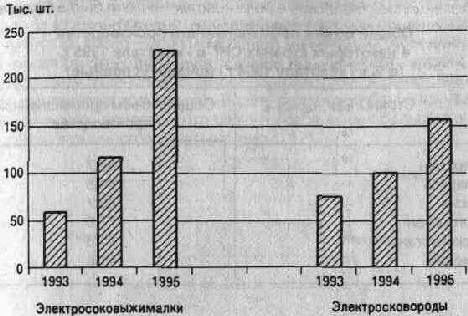
Рис. 5.10.

Область применения гистограмм и гистограмм одинакова, так как правила их построения идентичны. Одномерность изображаемых статистических показателей и их одномасштабность для различных столбиков и полос требуют выполнения единственного положения: соблюдения соразмерности (столбиков — по высоте, полос — по длине) и пропорциональности изображаемым величинам. Для выполнения этого требования необходимо: во-первых, чтобы шкала, по которой устанавливается размер столбика (полосы), начиналась с нуля; во-вторых, эта шкала должна быть непрерывной, т. е. охватывать все числа данного статистического ряда; разрыв шкалы и соответственно столбиков (полос) не допускается. Несоблюдение этих правил приводит к искаженному графическому представлению анализируемого статистического материала.

Например, давайте сравним гистограмму с предоставленной таблицей. 5.2 (рис. 5.11).

: Столбиковые и полосовые диаграммы как прием графического изображения статистических данных, по существу, взаимозаменяемы, т. е. рассматриваемые статистические показатели равно могут быть представлены как столбиками, так и полосами. И в этом, ^{и в} В другом случае для представления масштаба явления используется один размер каждого прямоугольника: высота столбца или длина полосы. Следовательно, сфера применения этих двух типов диаграмм по существу одинакова.

⁹ * Таблица 5.2

Общий объем промышленного производства в некоторых странах СНГ в 1 квартале 1995 г. (в % к I кварталу 1994 г.) (цифры условные)

Страны СНГ	Общий объем промышленного производства
Казахстан	88,7
Беларусь	83,5
Россия	80,7
Кыргызстан	77,6
Таджикистан	71,8
Армения	41,6

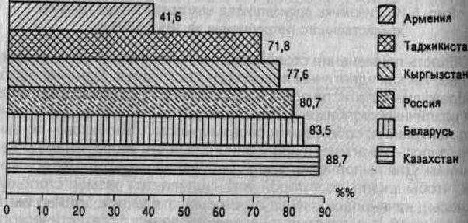
Рис. 5.11.

направленные диаграммы.

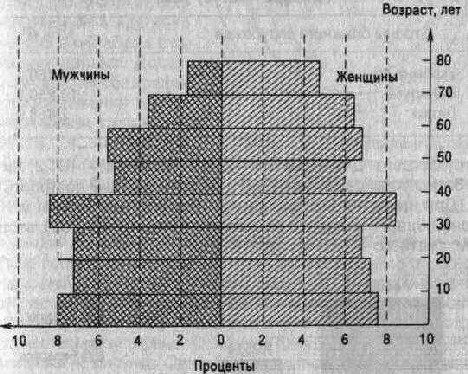
Рис. 5.12.

эти диаграммы выражают величину изображаемого явления размером своей площади.

Для получения схем рассматриваемого типа используются различные геометрические формы: квадрат, круг, реже прямоугольник. известно, что площадь квадрата равна квадрату его стороны, а площадь круга определяется пропорционально квадрату его радиуса. Поэтому для построения диаграмм необходимо сначала извлечь квадратный корень из сравниваемых значений. Затем

на базе полученных результатов определить сторону квадрата или радиус круга соответственно принятому масштабу

Например, если изобразить в виде квадрата или круга поставки российского газа в ближайшее зарубежье, то сначала нужно извлечь квадратные корни из этих цифр (табл. 5.3).

Таблица 5.3

Поставки российского газа в страны ближнего зарубежья, январь — август 1995 г.

Страны ближнего зарубежья	Млн. м 3
Украина Беларусь Литва	44460,1 10 250,0 2 458,0

Это составит: для Украины — 210,9; Беларуси — 101,2; Литвы -49,6. Затем установить масштаб и по этим данным построить квадраты. Для нашего примера примем 1см равным 30 млн. м ³ . Тогда сторона первого квадрата составит 7,03 см (210,9 : 30); второго-3,4 см; третьего — 1,65 см (рис. 5.13).

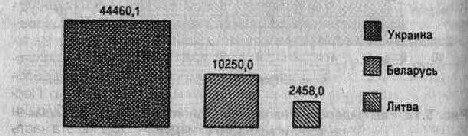
Рис. 5.13.

Для правильного построения диаграмм квадраты или круги должны быть размещены на одинаковом расстоянии друг от друга, и на каждом рисунке указать числовое значение, которое оно представляет, без указания шкалы измерений.

графическое изображение,

сравнения в

Важнейший признак любой диаграммы — масштаб. Поэтому, чтобы правильно построить фигурную диаграмму, необходимо определить единицу счета. В качестве последней принимается отдельная фигура (символ), которой условно присваивается конкретное численное

значение. И исследуемая статистическая величина представлена ​​отдельным количеством цифр одинакового размера, расположенных на рисунке последовательно. Однако в большинстве случаев невозможно представить статистический показатель целым числом цифр. Последнюю из них необходимо разделить на части, так как с точки зрения масштаба иероглиф — слишком большая единица измерения. Обычно эта часть определяется на глаз. Сложность точного определения этого — недостаток фигурных диаграмм. Однако, если в представлении статистических данных не требуется большей точности, результаты будут вполне удовлетворительными.

Рассмотрим построение фигурной диаграммы по данным табл. 5.4 фермерских хозяйств в России за 1993-1995 гг.

Таблица 5.4

Численность фермерских хозяйств в России за 1993 — 1995 гг.

(данные условные) (тыс.)

Год	1993	1994	1995
Численность фермерских хозяйств	49	183	270

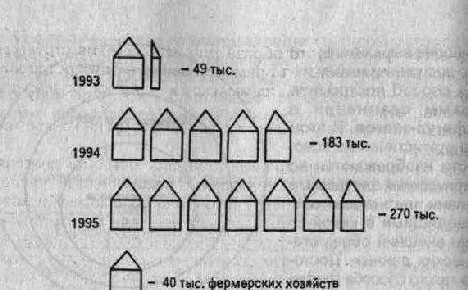
Рис. 5.15.

Примем условно за один знак 40 тыс. фермерских хозяйств. Тогда число хозяйств в России в 1993 г. в размере 49 тыс. будет изображено в количестве 1,22 хозяйства, в 1994 г. — 4,6 хозяйства и т. д. (рис. 5.15).

Обычно фигурные диаграммы широко используются для распространения статистики и рекламы.

4. Структурные диаграммы

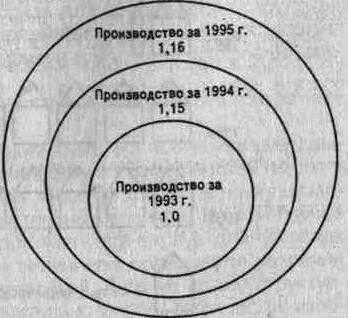
Основная цель структурных диаграмм — графически представить состав статистических совокупностей, характеризуемый как взаимосвязь между различными частями каждой из совокупностей. Состав статистической совокупности можно представить графически с использованием как абсолютных, так и относительных показателей. В первом случае не только размеры отдельных частей, но и размеры диаграммы в целом определяются статистическими значениями и изменяются в соответствии с вариациями последних. Во втором — размер всего графика не меняется (так как сумма всех частей любой совокупности составляет 100%), а меняются только размеры отдельных его частей. Графическое представление состава населения в виде абсолютных и относительных показателей способствует более глубокому анализу и позволяет проводить международные сравнения и сравнения социально-экономических явлений.

Прямоугольники используются в качестве графического изображения для представления структуры агрегатов — для создания гистограмм и столбчатых диаграмм и кругов — для создания круговых диаграмм.

Покажем построение указанных выше диаграмм на конкретных примерах.

Чтобы по приведенным данным табл. 5.5 построить диаграмму, отражающую структуру сравниваемых совокупностей по соотношению в них отдельных видов часов, ряд абсолютных показателей заменяется рядом относительных величин. В этом случае каждая из полос на диаграмме будет иметь одинаковую длину, поскольку переключение на относительные значения отменяет различия в абсолютных размерах популяций. В то же время структурные различия проявляются значительно четче. Графическое изображение структуры с помощью столбиковых (полосовых) диаграмм позволяет изучить особенности многих изучаемых экономических явлений. Так, приведенная на рис. 5.16 диаграмма, построенная по данным табл. 5.5, характеризует увеличение доли наручных часов в общем производстве.

Таблица 5.5

Производство часов по видам в одном из регионов России за 1985 — 1995 гг.

	198	5г.	199	5г.
	млн. шт.	%	млн. шт.	%
Часы, всего	52,5	100,0	60,1	100,0
В том числе:
наручные настенные	24,4 9,3	46,5 17,7	31,6 10,5	52,6 17,5
будильники	18,8	35,8	18,0	29,9

Более распространенный способ графического представления структуры статистической совокупности — круговая диаграмма, которая считается основной формой диаграммы для этой цели. Это потому, что идея целого очень хорошо и ясно выражена в круге, который представляет собой целое. Удельный вес каждой части совокупности в секторной диаграмме характеризуется величиной центрального угла (угол между радиусами круга).

Сумма всех углов круга, равная 360°, приравнивается к 100%, а следовательно, 1% принимается равным 3,6°.

Рис. 5.16.

Приведем пример построения секторной диаграммы по данным табл. 5.6.

Таблица 5.6

Динамика доли негосударственного сектора экономики в розничной торговле (в % к общему объему розничного товарооборота в России)

	—1—————-Г’ 1992г.	»,а о г Ч01.ИИ/ 1993 г.
Государственный сектор Негосударственный сектор	78 22	49
В том числе предприятия:		51
частной и смешанной форм
собственности
потребительской кооперации прочих форм собственности	1,8 20 0,2	31 16 4

Создание круговой диаграммы начинается с определения центральных углов секторов. Для этого процентное выражение отдельных частей совокупностей умножают на 3,6°. Например, для данных:

1992г.: 78

• 3,6° = 280,8°;
• 1,8

• 3,6° = 6,5°; 20
• 3,6° = 72°;

0,2

• 3,6° = 0,7°;

1993г.: 49-3,6° =176,4°; 31-3,6° = 111,6°; 16

• 3,6° = 57,6°;

4

• 3,6° = 14,4°.

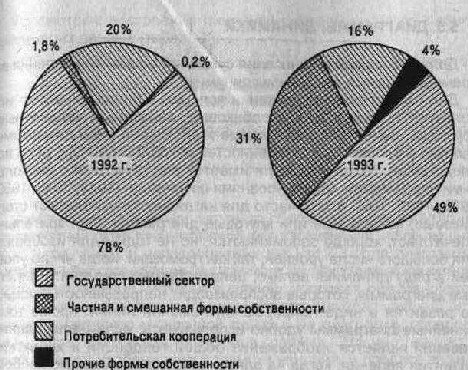
Рис. 5.17.

По найденным значениям углов круги делятся на соответствующие секторы (рис. 5.17).

Использование круговых диаграмм позволяет не только графически представить структуру населения и ее изменение, но и показать динамику численности этой популяции. Для этого строятся круги, пропорциональные объему исследуемого штриха, затем отдельные его части выделяются секторами.

Рассмотренные методы графического представления структуры населения имеют как достоинства, так и недостатки.

Таким образом, круговая диаграмма сохраняет ясность и выразительность только для небольшого числа частей популяции, в противном случае ее использование неэффективно. Кроме того, четкость круговой диаграммы снижается по мере изменения структуры отображаемых совокупностей: она становится больше, если в сравниваемых структурах есть существенные различия. Преимуществом столбиковых (ленточных) структурных диаграмм по сравнению с секторными являются их большая емкость, возможность отразить более широкий объем полезной информации.

5. Диаграммы динамики

Чтобы представить и оценить развитие явления во времени, строятся динамические диаграммы.

Для наглядного изображения явлений в рядах динамики используются диаграммы: столбиковые, ленточные, квадратные, круговые, линейные, радиальные и др. Выбор типа диаграммы зависит в основном от характеристик исходных данных, цели исследования. Например, если имеется ряд динамики с несколькими неравноотстоящими уровнями во времени (1913, 1940, 1950, 1980, 1985, 1997 гг.), то часто для наглядности используют столбиковые, квадратные или круговые диаграммы. Они впечатляют визуально, хорошо запоминаются, но не подходят для представления большого количества уровней, так как громоздки. При большом количестве уровней в динамическом ряду целесообразно использовать линейные диаграммы, воспроизводящие непрерывность процесса развития в виде непрерывной ломаной линии. Кроме того, линейные диаграммы удобно использовать: если целью исследования является изображение общей тенденции и характера развития явления; когда на одном графике необходимо изобразить несколько динамических рядов с целью их сравнения; если наиболее существенным является сопоставление темпов роста, а не уровней.

Для построения линейных диаграмм используется прямоугольная система координат. Обычно по оси абсцисс откладывается время (годы, месяцы и т. д. ), а по оси ординат — размеры изображаемых явлений или процессов. На оси ординат наносят масштабы. На их выбор стоит обратить особое внимание, так как от этого зависит общий вид графика. Обеспечение равновесия, пропорциональности между осями координат необходимо в графике в связи с тем, что нарушение равновесия между осями координат дает неправильное изображение развития явления;

— Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в динамике явлений мало выделяются, и наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колебания. Одинаковые периоды времени и размер уровня должны совпадать с одинаковыми сегментами шкалы.

В статистической практике часто используются графические изображения с едиными масштабами. По оси абсцисс они отложены пропорционально количеству периодов времени, а по оси ординат — пропорционально самим уровням. Масштабом равномерной шкалы будет длина отрезка, принятого за единицу рассмотрим построение линейной диаграммы на основании следующих данных (табл. 5.7).

Таблица 5.7

Динамика валового сбора зерновых культур в регионе за 1985-1994 гг.

Год	1985	1986	1987	1988	1989	1990	1991	1992	1993	1994
Млн.т	237,4	179,2	189,1	158,2	186,8	192,2	172,6	191,7	210,1	211,3

Изображение динамики валового сбора зерновых культур на координатной сетке с неразрывной шкалой значений, начинающихся от нуля, вряд ли целесообразно, так как 2/3 поля диаграммы остаются неиспользованными и ничего не дают для выразительности изображения. Поэтому в данных условиях рекомендуется строить шкалу без вертикального нуля, т. е. шкала значений разрывается недалеко от нулевой линии и на диаграмму попадает лишь часть всего возможного поля графика. Это не приводит к искажениям в изображении динамики явления, и процесс его изменения рисуется диаграммой более четко (рис. 5.18).

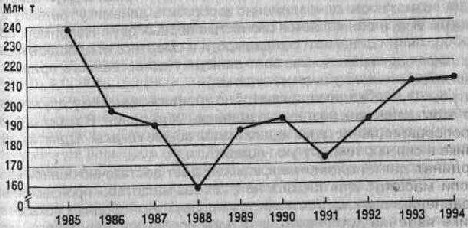
Рис. 5.18.

Часто на линейном графике представлено несколько кривых, которые дают сравнительную характеристику динамики различных индикаторов или одного и того же индикатора.

Примером графического изображения сразу нескольких показателей является рис. 5.19.

141

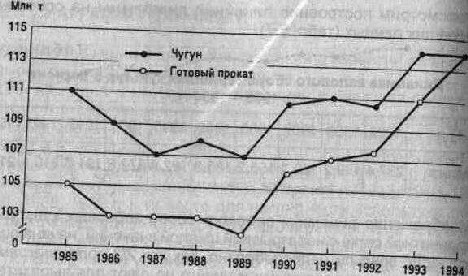
Рис. 5.19.

Однако на графике следует размещать не более трех-четырех кривых, так как их большое количество неизбежно усложняет рисунок, а линейная диаграмма теряет четкость.

В некоторых случаях построение двух кривых на графике позволяет одновременно представить динамику третьего индикатора, если это разница между первыми двумя. Например, при описании динамики рождаемости и смертности площадь между двумя кривыми показывает величину естественного прироста или убыли населения.

Иногда возникает необходимость сравнить динамику двух индикаторов с разными единицами измерения на графике. В таких случаях понадобится не одна, а две масштабные шкалы. Одну из них размещают справа, другую — слева.

Однако такое сравнение кривых не дает достаточно полного представления о динамике этих показателей, поскольку шкалы произвольны. Поэтому сравнение динамики уровня двух разнородных показателей должно производиться на основе использования одной и той же шкалы после преобразования абсолютных значений в относительные. Примером такой линейной диаграммы является рис. 5.20.

Линейные диаграммы с равномерным масштабом имеют недостаток, который снижает их познавательную ценность: единый масштаб позволяет измерять и сравнивать только абсолютные увеличения или уменьшения показателей, показанных на графике, за период исследования. Однако при изучении динамики важно знать относительные изменения исследуемых показателей по сравнению с достигнутым уровнем или темпы их измене-

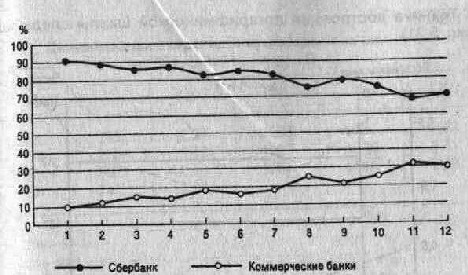
Рис. 5.20.

ния. Именно относительные изменения экономических показателей в динамике искажаются при отображении на координатной диаграмме с равномерным вертикальным масштабом. Более того, в обычных координатах он теряет всякую ясность и даже становится невозможным визуализировать ряд динамики с резко меняющимися уровнями, которые обычно возникают во временных рядах в течение длительного периода времени.

В этих случаях следует отказаться от единой шкалы и строить график на основе полулогарифмической системы. Основная идея полулогарифмической системы состоит в том, что равным значениям логарифмов чисел соответствуют равные линейные отрезки. Преимущество этого подхода в том, что он позволяет уменьшить размер больших чисел за счет их логарифмических эквивалентов. Однако со шкалой в виде логарифмов график сложно понять. рядом с логарифмами, указанными на шкале, необходимо поставить те же числа, которые характеризуют уровни воображаемого динамического ряда, соответствующие номерам указанных логарифмов. Эти типы диаграмм называются диаграммами с полулогарифмической сеткой.

Полулогарифмической сеткой

Техника построения логарифмической шкалы следующая (рис. 5.21).

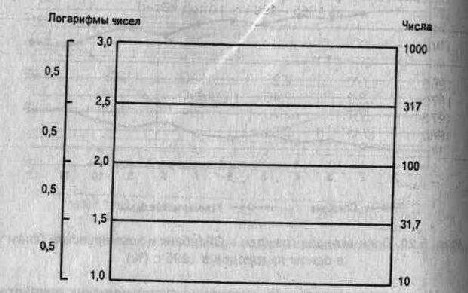
Рис. 5.21.

Необходимо найти логарифмы исходных чисел, начертить ординату и разделить ее на несколько равных частей. Затем нанести на ординату (или равную ей параллельную линию) отрезки, пропорциональные абсолютным приростам этих логарифмов. Далее записать соответствующие логарифмы чисел и их антилогарифмы, например (0,000; 0,3010; 0,4771; 0,6021; …; 1,000, что дает 1, 2, 3, 4, …, 10).

Полученные антилогарифмы окончательно дают вид искомой шкалы на ординате.

Приведем пример логарифмического масштаба. : Допустим, что надо изобразить на графике динамику производства электроэнергии в регионе за 1965-1994 гг., за эти годы оно выросло в 9,1 раза. С этой целью находим логарифмы для каждого уровня ряда (табл. 5.8).

‘ Определив минимальное и максимальное значение логарифмов производства электроэнергии, построим масштаб с таким расчетом, чтобы все данные разместились на графике.

Учитывая масштаб, находим соответствующие точки, которые соединим прямыми линиями, в результате получим график (рис. 5.22) с использованием логарифмического масштаба на оси ординат. Он называется диаграммой на полулогарифмической сетке. Полной логарифмической диаграммой он станет в том случае, если по оси абсцисс будет построен логарифмический масштаб. В ря

Таблица 5.8

Динамика производства электроэнергии в регионе за 1965 -1994 гг. (млрд. кВт.ч)

Год	У	1-дУ,	Год	У,	1-9У,
1965 1970 1975	170 292 507	2,23 2,46 2,70	1985 1990 1994	1039 1294 1544	3,02 3,11 3,19
1980	741	2,84

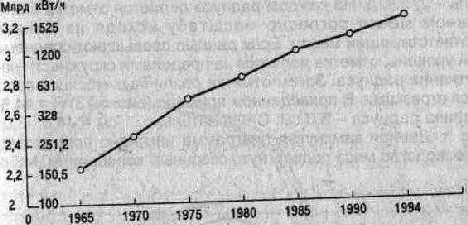
Рис. 5.22.

дах динамики это никогда не применяется, так как логарифмирование времени лишено всякого смысла.

Применяя логарифмический масштаб, можно без всяких вычислений характеризовать динамику уровня. Если кривая на логарифмическом масштабе несколько отклонена от прямой и становится вогнутой к оси абсцисс, значит, имеет место падение темпов; когда кривая в своем течении приближается к прямой — стабильность темпов; если она отклоняется от прямой в сторону, выпуклую к оси абсцисс, изучаемое явление имеет тенденцию к росту с увеличивающимися темпами.

радиальные диаграммы,

Замкнутые диаграммы

спиральными.

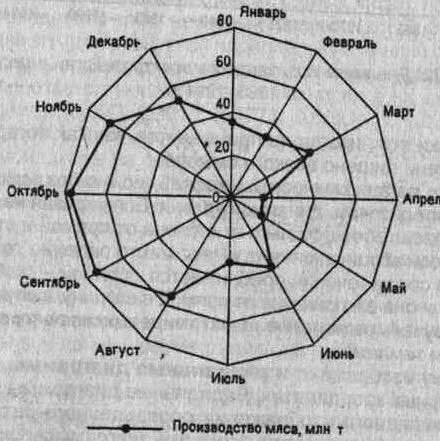
Рис. 5.23.

Построение спиральных диаграмм отличается от замкнутых тем, что в них декабрь одного года соединяется не с январем данного же года, а с январем следующего года. Это дает возможность изобразить весь ряд динамики в виде спирали. Особенно наглядна такая диаграмма, когда наряду с сезонными изменениями происходит неуклонный рост из года в год (рис. 5.24).

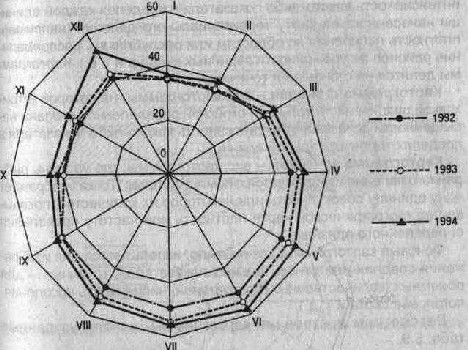
Рис. 5.24.

моделью Лоренца, или кривой Лоренца.

6. Статистические карты , Статистические карты

Средствами изображения территориального размещения являются штриховка, фоновая раскраска или геометрические фигуры. Различают картограммы и картодиаграммы.

Картограмма, Картограмма фоновая -, Картограмма точечная

Фоновые картограммы, как правило, используются для изображения средних или относительных показателей, точечные — для объемных (количественных) показателей (численность населения, поголовье скота и т. д.).

Рассмотрим построение картограммы, используя данные табл. 5.9.

Таблица 5.9

Плотность населения восьми районов области (цифры условные)

№ района	1	2	3	4	5	6	7	8
Плотность населения
человек	3,0	4,0	11,0	14,0	17,0	13,0	11,0	3,0

Прежде чем приступить к построению картограммы, необходимо разбить районы на группы по плотности населения, а затем установить для каждой определенную окраску или штриховку.

Согласно данным табл. 5.9 все районы по плотности населения можно разбить на три группы: 1) районы, имеющие плотность населения до 4 тыс. человек; 2) от 4 до 12 тыс. человек; 3) от 12 до 17 тыс. человек. Тогда к первой группе относятся районы № 1, 8; ко второй — № 2, 3, 7; к третьей — № 4, 5, 6. Если принять для каждой группы районов окраску различной насыщенности, то на фоновой картограмме хорошо видно, как располагаются на территории области отдельные районы по плотности населения (рис. 5.25).

Другим примером фоновой картограммы является рис. 5.26.

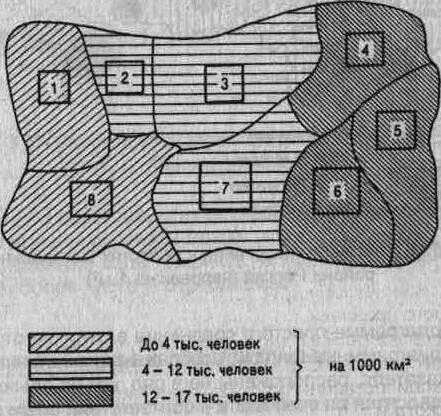
Рис. 5.25.

картодиаграммы,

Среди картодиаграмм следует выделить картодиаграммы простого сравнения, графики пространственных перемещений, изолиний.

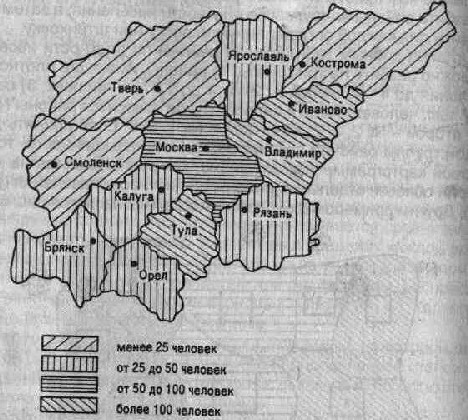
Рис. 5.26..

На картодиаграмме простого сравнения в отличие от обычной диаграммы диаграммные фигуры, изображающие величины исследуемого показателя, расположены не в ряд, как на обычной диаграмме, а разносятся по всей карте в соответствии с тем районом, ^областью или страной, которые они представляют. ‘» ‘Элементы простейшей картодиаграммы можно обнаружить на ‘Политической карте, где города отличаются различными геометрическими фигурами в зависимости от числа жителей.

В качестве примера картодиаграммы возьмем изображение валового сбора зерна Центрального района России (рис. 5.27).

Изолинии (от греч. 1зоз — равный, одинаковый, подобный) -это линии равного значения какой-либо величины в ее распространении на поверхности, в частности на географической карте или графике. Изолиния отражает непрерывное изменение исследуемой величины в зависимости от двух других переменных и применяется при картографировании природных и социально-экономических явлений. Изолинии используются для получения ко-

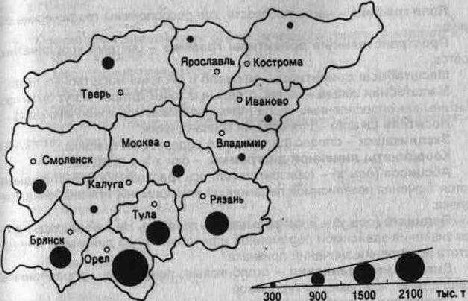
Рис. 5.27.

Перечисленные виды графиков не являются исчерпывающими, но они наиболее часто употребляемы.

Литература

[Электронный ресурс]//URL: https://management.econlib.ru/referat/na-temu-statisticheskie-grafiki-i-tablitsyi/

1.Елисеева И.И., Юзбашев М.М. Общая теория статистики

2.Ряузов Н.Н. Общая теория статистики

3.Теория статистики под ред. Шмойловой Л.А.

© Реферат плюс